Elucidating the loose tie between precipitation and streamflow sensitivities to warming across the contiguous United States

Abstract

The relation of regional precipitation and streamflow sensitivities to warming is complicated by runoff often being the small residual in the balance between precipitation and evapotranspiration. In addition, the inhomogeneous nature of land-hydrological properties and hydrological interventions by humans, like irrigation and dams, have made streamflow sensitivities challenging to constrain with both climate models and observations. Here, we elucidate the hydrological processes driving the regionally varying mean and extreme streamflow sensitivities to warming across the contiguous United States in a counter-factual warming scenario using GFDL’s moderately high-resolution global climate model. We show that over the West Coast and eastern US, atmospheric rivers are the dominant driver of high-flows in the present climate and of more frequent high-flows in a warmer climate. Over the mountainous western US, streamflows dwindle despite increases in precipitation and antecedent soil moisture, as loss of snow fuels evapotranspiration at double the rate of precipitation changes.

Introduction

Understanding how regional precipitation and river floods respond to increasing temperatures is a crucial question for climate science, as it has severe implications for the mitigation of natural hazards that cost lives and property¹. In the United States, the contribution of historical precipitation changes to flood damages has been estimated to be an accumulative $73 billion², highlighting the need for a better understanding of the relation of regional precipitation and flood changes under warming. At global scales strong constraints on precipitation changes with warming exist with an expected mean increase of 2–3% K^{−1 3,4,5,6}, large-scale patterns following the paradigm of wet gets wetter, dry gets drier^3,7,8,9 and an overall shift towards more extreme and less moderate precipitation events^{10,11,12,13,14,15,16,17}; a change in the character of precipitation¹⁸. However, at regional scales vast uncertainties remain as precipitation changes over land are more complex than wet gets wetter, dry gets drier¹⁹ and a computational need remains for compromising between spatial resolution of climate models, long integration times and ensemble or domain sizes^{16,20,21,22,23}, as well as limitations in process understanding^6,24,25,26.

While these constraints also limit predictability of changes in river floods with warming, precipitation is only one of a multitude of land-hydrological processes that determine flooding and its change with warming^27,28,29,30. The amount of precipitation necessary to produce runoff is strongly determined by antecedent soil conditions, which are controlled by processes such as previous precipitation, snow-melt and evapotranspiration (ET)^31,32,33,34 that in climate models often require strong assumptions about the sub-grid scale. In addition, observational constraints on trends in river floods remain limited due to weak signal-to-noise ratios and human interventions^35,36. Hence, improving global coupled atmosphere-land models to higher resolutions offers an exciting opportunity to enhance our process understanding of precipitation and flood changes with warming.

Recent advances to moderately high resolutions of 50 km and higher driven through the CMIP6-HighResMIP initiative³⁷ have shown promising improvements in representing precipitation and its extremes^{38,39,40,41,42,43,44}, particularly in the mid-latitudes where mesoscale frontal systems often dominate the spatial scales of precipitation^45,46. A strong contributor to mid-latitude precipitation and floods are atmospheric rivers (ARs)^{16,32,47,48,49,50}, which are characterized as elongated narrow bands of intense poleward moisture transport and typically associated with extra-tropical cyclones^47,51,52. Previous studies point to a substantial improvement in the representation of AR precipitation in moderately high-resolution models and highlight AR precipitation changes with warming that account for a significant fraction of the total mid-latitude precipitation response, especially over the United States^{45,46,49,53,54,55,56}. Despite this, initial assessments of moderately high-resolution models for hydrological applications are limited. Recent first results show promise in capturing peak annual runoff over the central US, with needs for downscaling and bias correction remaining to accurately assess local scales⁵⁷.

Here, we further explore the new opportunities provided by moderately high-resolution to assess changes in river floods and their drivers with warming, distinguishing AR and non-AR precipitation, as well as snow melt, across the contiguous United States (CONUS). We utilize the global coupled atmosphere-land model AM4.0/LM4.0^58,59 with a resolution of 50 km⁴⁶ developed at the Geophysical Fluid Dynamics Laboratory (GFDL), which has shown promising capabilities in capturing mean and extreme precipitation^45,46,58. LM4.0 discharges surface and sub-surface runoff across a grid-scale river network (Supplementary Fig. S1) as fluxes of liquid water, ice and heat to connected grid-cells^60,61. This approach benefits from the grid-scale coupling of hydrological processes across river, land and atmospheric domains, allowing for a definitive attribution of various hydrological drivers of high river streamflows indicative of flooding and hence a process-based understanding of their sensitivity to warming.

Our experimental setup (detailed in the section “Model setup and simulations”) is designed to isolate the best constrained components of precipitation changes with warming, providing a sound basis for assessing the relation of changes in precipitation and streamflows. First, we isolate the thermodynamic precipitation response to warming, which excludes any changes in atmospheric winds and denotes the most significant and well-understood part of how precipitation extremes^12,24,62 and AR precipitation^49,63,64,65 change with warming. We achieve this by tightly nudging atmospheric winds toward NCEP reanalysis data⁶⁶ for both a control and a counter-factual warming simulation that we run over the historical period of 1951 to 2020. The control simulation (CTRL) follows the CMIP6 HighResMIP protocols³⁷ and is forced by observed daily sea surface temperatures (SSTs). The counter-factual warming simulation only differs in SST forcing by a homogeneous increase of SSTs across the global ocean by 2 Kelvin (P2K). Besides isolating the most significant and well-constrained parts of the total precipitation response to warming, our nudging approach also minimizes uncertainty arising from natural climate variability as well as dynamically driven model biases (see Supplementary Fig. S2), enhancing applicability to hydrological applications. In addition, we obtain a day-by-day comparability between the CTRL and P2K simulations as well as with observations (Supplementary Figs. S3 and S4), which we exploit in the section “Relative importance of changes in antecedent upstream soil moisture and water inputs”.

To elucidate the relationship of precipitation and streamflow changes with warming across CONUS, we first quantify their sensitivities to warming on the mean and in the extremes in the section “Precipitation and streamflow changes with warming”. We then identify high streamflows and investigate changes in their frequency with warming across CONUS, which we characterize by examining three inter-related conditions for high-flows. Firstly, we attribute high-flows to different upstream water inputs and their changes with warming in the section “Attribution to upstream precipitation and snow melt”, distinguishing AR and non-AR precipitation as well as snow-melt (as described in the section “Attribution to upstream precipitation and snow melt”). Secondly, we examine changes in water and energy constraints on losses through ET and runoff in the section “ Attribution to seasonal constraints on evapotranspiration”, highlighting seasonal constraints on the high-flow response. Thirdly, we discuss how these constraints are imprinted on antecedent soil moisture conditions prior to high-flows and to what degree these explain changes in high-flows compared to changes in upstream water inputs in the section “Relative importance of changes in antecedent upstream soil moisture and water inputs”. We draw final conclusions in the section “Discussion”.

Results

Precipitation and streamflow change with warming

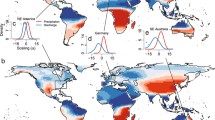
Figure 1 summarizes the thermodynamically driven changes in precipitation and streamflows across CONUS with warming in our counter-factual warming experiment. The thermodynamic precipitation response manifests as an overall increase across most of CONUS with an average of 3.6% K⁻¹ (with respect to the global mean warming signal in 2 m temperature), except in the dry southern states Arizona and New Mexico (Fig. 1a). To give some reference to this number, observed scaling of annual mean precipitation over CONUS between the years 1901 and 2015 is estimated at 4%⁶⁷, which given an increase in global mean 2 m temperature in that time of about 1.1 K⁶⁸ translates to a scaling of exactly 3.6% K⁻¹. Given the idealized assumptions of our experiment about constant atmospheric winds and the ignored direct effects of greenhouse gases^20,69, we have to acknowledge that we obtain the same number for different reasons. However, comparability to the observed mean precipitation response increases the applicability of our results.

Fig. 1: Regional contrasts in precipitation and streamflow sensitivities to warming.

Changes with warming in a mean precipitation, b extreme precipitation, c mean AR precipitation, d mean streamflow and e extreme streamflow across CONUS based on counter-factual warming experiment (see the section “Model setup and simulations”). “Extreme” refers to the 99.7th percentile of daily values, resembling events with an annual recurrence rate, also indicated by black vertical line in (f). Hatched regions denote insignificant changes of the mean as determined by z-test with critical value z = 1. f Shows relative change with warming in precipitation, AR precipitation and streamflow deduced for each grid-point as function of percentile and then averaged across CONUS (black) and for streamflow also across the west coast (green), the mountainous west (red) and the eastern US (blue) defined by zonal bounds at 120°W and 100°W, respectively, indicated by gray dashed lines in (e). Shading denotes standard error across respective region. Red solid line indicates Clausius–Clapeyron (CC) scaling of 7% K⁻¹.

To consider changes in extreme precipitation, we define extreme precipitation as the 99.7th percentile of daily precipitation which represents an average recurrence rate of once per year as commonly used in studies of hydrological extremes^70,71,72,73. Changes in extreme precipitation (Fig. 1b) are positive across CONUS and at 5.4% K⁻¹ generally larger than mean changes, with many local exceedances of the Clausius-Clapeyron (CC) scaling at 7% K^{−1 18,74,75}, highlighting the expected shift towards more intense precipitation^{10,11,12,13,14,15,16,17}. Mean AR precipitation changes (Fig. 1c, see the section “Atmospheric river detection and evaluation” on AR detection) fall between mean and extreme precipitation changes at an average of 4.2% K⁻¹. We want to emphasize that these scalings are not contradicting previously reported super-CC scaling of AR precipitation^76,77, which stems from a focus on sub-daily timescales while here we focus on daily timescales. We do, however, find a strong regional pattern in extreme AR-precipitation scaling with warming, with some local exceedances of CC-scaling across the mountainous west, somewhat resembling the lee-side of the Sierra Nevada, the Cascades and the Rocky Mountains. These results indicate a weakening of the orographic rain shadow with warming, which has previously been predicted from theory⁷⁸ and high-resolution regional modeling studies^79,80,81 and is therefore encouraging to identify in our moderately high-resolution simulations.

The warming response of mean and extreme river streamflows (Fig. 1d and e) strongly differs in its pattern and magnitude from the precipitation response, reflective of the streamflow response being controlled by a multitude of hydrological processes such as antecedent soil conditions and ET^{31,34,54,82,83,84,85,86}. Most prominently, mean and extreme streamflows decline over the mountainous western US (regions indicated by gray dashed lines in Fig. 1e and colored text below) in the presence of significant precipitation increases, particularly from ARs. Streamflow declines under warming have previously been noted and linked to the dominance of spring-time snow melt in driving hydrographs^{29,30,72,87,88,89}. Other, more regional studies have identified pronounced increases in evaporative demand⁹⁰ and ET⁹¹ across the southwestern US as drivers of drought and dwindling streamflows. Outside the mountainous west, streamflows increase with precipitation; however, the increase is significantly stronger over the east than over the west coast (Fig. 1e, note that we consider large parts of California towards the mountainous west, as we orient our regional definition based on the streamflow response).

We summarize the regional discrepancies of extreme precipitation and streamflow changes with warming across sub-regions of CONUS in Fig. 1f through mean relative changes in percentiles (following previous studies^20,34,92). The graphs can be interpreted as the regional mean change of daily precipitation or streamflow at a given recurrence rate described through the percentile on the x-axis (e.g. annual recurrence resembled through the 99.7th percentile of daily values). We find that precipitation changes show an expected increased sensitivity to warming at higher percentiles^6,12,20, with AR precipitation being more sensitive than total precipitation^45,55,56,93, approaching CC-scaling for the strongest extremes. Streamflows, however, show a much different behavior in their scaling across percentiles, representative of their loose tie to precipitation. On the one hand, we find an exceedance of precipitation changes by streamflow changes over the eastern US across all percentiles, which exceeds CC-scaling at percentiles >98. Over the mountainous west, on the other hand, streamflows dwindle across the distribution and, even at the highest percentiles, where precipitation increases the most. Streamflow changes over the West Coast lie between the other two regions, with generally positive changes but at a lower magnitude than CONUS-averaged precipitation changes.

Changes in the surface water balance

We can understand the regional variation in streamflow sensitivities to warming by considering the regionally integrated surface water balance and its changes with warming. The local surface water balance can be expressed as

$$P=ET+R+\Delta S$$

(1)

At any location, the local input of water through precipitation P is balanced by losses through ET, runoff R and a change in water storage on land ΔS. The local river streamflow is determined by the streamflow from upstream and the local runoff; in our model, the river does not feed water back to its surrounding soil^59,61. Figure 2a depicts the regionally and annually averaged terms of the surface water balance in the CTRL simulation (circles) normalized by the regional mean P. For reference, Fig. 2a also shows observationally deduced estimates of the regional surface water balance (crosses) obtained from a 1 km resolution Thornthwaite-style water balance model⁹⁴ that is forced by daily observations of precipitation and temperature^95,96,97 (detailed in the section “Evaluation of the surface water balance”).

Fig. 2: Regional differences in surface water balance.

a Shows regional annual average (1980–2020) terms of the surface water balance (Eq. (1)) in the CTRL simulation (circles) and observationally deduced based on a surface water balance model⁹⁵ (crosses), normalized by the regional mean precipitation P to make different regions comparable. b Shows the respective change with warming in each of the terms, normalized by the global mean warming response. Note that changes in b show absolute changes of the budget terms in units of % K⁻¹ due to normalization by P. Errorbars denote spatial standard deviation within the respective regions.

We find that the partitioning of ET and R across the three regions is vastly different, with R/P denoting only 18% over the mountainous West, 28% over the eastern US and 51% over the west coast. Over the mountainous west and eastern US, these numbers are in remarkably good agreement with the observationally deduced estimates, while over the west coast, R is underestimated by our model, and ET is overestimated. We attribute this bias to overestimated ET/P over major mountain ranges, such as the Sierra Nevada and the Cascades, which are not sufficiently resolved in our 50 km simulations (Supplementary Fig. S5). Underestimated orographic lift yields underestimated P in mountainous terrain, where ET is generally less efficient due to enhanced partitioning to snow and lower temperatures. These effects bias our regional water balance over the west coast to enhanced ET/P and reduced R/P compared to observations in Fig. 2a. The inability of the CTRL simulation to capture strong horizontal gradients in R and ET also explains the underestimated spatial standard deviations over the west coast and the mountainous west. Nonetheless, the model captures the major variability of R and ET partitioning between the three regions, although there should be awareness towards the underestimated R over the west coast.

The strong differences in partitioning of R and ET across the three regions imply that for a given change in the partitioning of ET and R, the relative change in R, and hence streamflows, is most sensitive over the mountainous west and the least sensitive over the west coast. Fig. 2b shows the absolute change in the partitioning of ET, R and S with respect to P with warming, highlighting the varying responses of each region. We find no noticeable changes over the west coast, in agreement with a scaling of R and streamflows to mostly follow changes in P. Over the mountainous west, we find a substantial increase in ET/P that is balanced by a similar decrease in R/P, explaining the strong relative reduction in streamflows found in Fig. 1d. Over the east, ET/P decreases while R/P increases accordingly, explaining how the diagnosed streamflow increases over the east exceed the increases in P.

Attribution to upstream precipitation and snow melt

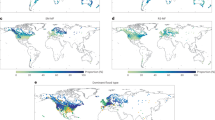
We now further characterize the physical causes for the diagnosed disconnect of precipitation and streamflow changes across CONUS, with particular focus on high-flows. In the following, we identify high-flows as days exceeding the long-term 99.7th percentile of daily streamflow (once-per-year recurrence) based on the CTRL simulation and attribute changes in high-flow frequency with warming to changes in upstream AR precipitation, non-AR precipitation, and snow melt across CONUS (see method in the section “Attribution of high-flows to upstream drivers” and Supplementary Fig. S6). We first consider maps of the long-term mean high-flow frequency in Fig. 3 and then point out the regionally varying seasonalities of high-flows and their drivers in Fig. 4.

Fig. 3: Regionally varying upstream drivers of high-flows.

a, c and e show fraction f_driver of high-flow events attributed to AR-precipitation events, non-AR precipitation events and snow melt events, respectively, relative to the total number of attributed high-flows based on CTRL simulation (following the attribution method described in the section “Attribution of high-flows to upstream drivers”). b, d and f, show relative changes in the respective f_driver with warming based on P2K-CTRL, normalized by the global mean warming signal. Model results are averaged over HUC4 hydrological sub-regions⁹⁸, the outline of which is colored by belonging large-scale region of the west coast (green), the mountainous west (red) and the eastern US (blue).

Fig. 4: Varying high-flow seasonality by region and upstream driver.

a, c, e and g show regionally and monthly averaged seasonal cycles of high-flow occurrence rates in CTRL simulation, respectively for total high flow events, AR precipitation events, non-AR precipitation events and snow melt events. b, d, f and h show the respective absolute changes with warming, normalized by the global mean warming signal.

The left column of Fig. 3 shows the fraction f_driver of high-flow events attributed to specific upstream liquid water inputs relative to the total number of attributed high-flow events. The results of the attribution are aggregated over hydrological sub-regions defined through 4-digit hydrological unit codes by the US Geological Survey (USGS)⁹⁸. The separation of hydrological drivers of high streamflows follows a remarkably similar spatial pattern as streamflow changes with warming (Fig. 1d and e), indicative of the hydrological driver being a good predictor of the change in streamflow with warming. We find on the one hand that over both the West Coast and eastern US, liquid precipitation is the major driver of high-flows, with AR precipitation exceeding non-AR precipitation in most sub-regions. On the other hand, melt is found as the exclusive driver of high-flows across the mountainous west, also contributing up to 20% towards high-flow events over some sub-regions of the west coast, like the Sacramento River basin and New England in the eastern US. Note that we also assessed events of combined (AR-) precipitation and melt for cases where a single driver cannot be attributed to a high-flow. However, since we find only relatively few of such combined events (see Supplementary Fig. S7), we excluded further analysis from the scope of the paper, which focuses on the first-order regional variance within CONUS. We additionally want to point out that the results presented in this section are not sensitive to the choice of at least one different AR tracking algorithm (see the section “Atmospheric river detection and evaluation” and Supplementary Figs. S8 and S9).

The right column of Fig. 3 shows the change in the number of high-flow days induced by the respective hydrological drivers with warming in our P2K experiment relative to the CTRL experiment. The pattern of these changes largely resembles the pattern of overall streamflow changes diagnosed in Fig. 1d and e. We find an increasing number of high-flow days across the west coast and the eastern US that we can now attribute to both AR precipitation and, to a slightly lower degree, non-AR precipitation. Over the mountainous west, we identify a strong reduction in melt-induced high-flows that regionally exceeds −30% K⁻¹. This reduction in melt-driven high-flows occurs despite strong increases in precipitation over the mountainous west, particularly from ARs (Fig. 1). To start exploring why the reduction in melt-driven high-flows over the mountainous west is not buffered by increases in precipitation-driven high-flows, while precipitation-driven high-flows on the west coast and the eastern US amplify, we now take a seasonal perspective at the changes in high-flows and their drivers. This enables a more process-oriented understanding when connecting these results to changes in land-hydrological constraints on ET in the next section.

Figure 4 shows the regionally and monthly integrated fraction ${f}_{{\rm{driver}}}^{{\rm{mon}}}$ of high-flows relative to the annual sum of total attributed high-flows for the CTRL simulation (left column) and the P2K−CTRL difference normalized by the global mean warming signal (right column). The seasonality of total high-flows found in the CTRL simulation (Fig.4a) differs significantly between the three regions. Over the West Coast, high flows occur most frequently in winter months with a maximum in February. As expected for the west coast⁹⁹, the attribution to upstream drivers reveals that the majority of these winter events are driven by ARs, with non-AR precipitation playing a secondary role in winter and melt becoming more significant in March. Over the mountainous West, high-flow occurrence peaks in March and is found to be exclusively driven by melt. Over the eastern US, the seasonality is less confined than in the other regions, with a broader peak around May. ARs contribute 60% of high-flows throughout spring, while non-AR events become more significant towards summer.

These regional seasonalities of high-flows change under warming (right column of Fig. 4). Over the west coast, the seasonality becomes more pronounced with more frequent high-flows in winter months and less frequent high-flows in spring, driven by more frequent AR-driven high-flows and less frequent melt-driven high-flows. Over the eastern US, high-flow frequency increases throughout the year with a less pronounced maximum in spring, weakening the seasonality of high-flow occurrence with warming. Over the mountainous west, high flows diminish with warming at a rate that is proportional to the monthly climatological high-flow frequency, also implying a weakened seasonality. It is worth noting that the near-zero change in precipitation-driven high-flows at the annual mean level over the mountainous west (Fig. 3b and d) holds true for the monthly level, i.e., there are no compensating changes in precipitation-driven high-flows between different months, despite the previously diagnosed increases in mean and extreme precipitation. This motivates examination of further constraints on high-flows, such as changes in the seasonal surface water balance that we discuss in the next section.

Attribution to seasonal constraints on evapotranspiration

We now explore how changes in energy and water constraints on ET with warming help explain changes in the regional variability in changes of the partitioning between ET and R, as identified in Fig. 2b, and hence the warming response of high-flows. We start by considering annual mean maps of the annual mean dryness index ${\mathcal{D}}$ and evaporative index ${\mathcal{E}}$ (as commonly used in Budyko analysis^100,101):

$${\mathcal{D}}={{PET}}/P$$

(2)

$${\mathcal{E}}={{ET}}/P$$

(3)

where PET refers to potential ET, i.e., the energetic upper bound on ET (see the “Methods” subsection “Calculation of potential evapotranspiration”). An annual mean ${\mathcal{D}} < 1$ indicates that ET is energy limited, while ${\mathcal{D}} > 1$ indicates that ET is water limited. Figure 5a shows that annual mean ${{\mathcal{D}}}_{{\rm {CTRL}}}$ follows a somewhat similar spatial pattern as the streamflow response to warming (Fig. 1d and e), with a strong zonal gradient between energy-limited ET in the eastern US and some parts along the west coast, and a water-limited mountainous west with pronounced aridity in the south-west. This general pattern is in agreement with downscaled reference datasets^102,103,104.

Fig. 5: Energy and water constraints on changes in seasonality of surface water balance.

a Shows annual mean map of ${\mathcal{D}}$ in CTRL simulation, where PET is derived from Penman–Monteith equation over an open water surface (see the “Methods” subsection “Calculation of potential evapotranspiration”). ${\mathcal{D}} <$1 indicates energy limitation of ET, and ${\mathcal{D}} >$1 indicates water limitation of ET. b Shows annual mean change in ${\mathcal{E}}$ with warming, indicating whether ET or P is more enhanced with warming. c–h Show relative changes of mean seasonal cycle c in P, d in ET, e in ${{\mathcal{E}}}_{{\rm {m}}}$ (Eq. (5)), f in ${{\mathcal{D}}}_{{\rm {m}}}$ (Eq. (4)), g in F_net, normalized by specific heat of vaporization ${{\mathcal{H}}}_{{\rm {vap}}}$ and ET_CTRL, h in R. Relative changes are calculated after spatial averaging.

With an energetic surplus in evaporative potential across the mountainous west, ET is found to increase at a higher rate than over the west coast or eastern US, as implied by a positive change in ${\mathcal{E}}$ shown in Fig 5b. As previously discussed in the section “Precipitation and streamflow changes with warming”, the increase in ${\mathcal{E}}$ across the mountainous west implies a shift of the surface water balance towards overall drier conditions with reduced R. Over the eastern US a slight opposite shift towards enhanced R is found and over the west coast ${\mathcal{E}}$ changes are only slightly positive. These energetic constraints on annual mean ET align well with the diagnosed annual mean changes in streamflows in Fig. 1.

To more closely examine how the discussed annual mean changes in ${\mathcal{D}}$ and ${\mathcal{E}}$ occur in different regions, we now turn to the seasonal perspective and first consider changes in ET and P (Fig. 5c and d). All regions exhibit a pronounced seasonality in P changes with warming, where winter P increases at a higher rate than summer P. This seasonality is particularly pronounced over the mountainous west, where mean P increases at around 6% K⁻¹ in winter and reduces in July and August at around −1% K⁻¹. The seasonality in changes of ET (Fig. 5d) is similarly phased as P; however, the relative increase in ET with warming is about double the relative increase in P over the mountainous west and also around one third higher over the west coast in winter, while it is slightly weaker over the east.

To consider monthly changes in ${\mathcal{D}}$ and ${\mathcal{E}}$, we define them to more appropriately represent the water available for ET on the monthly timescale, which is rather the sum of liquid precipitation P_l and melt M than total precipitation P:

$${{\mathcal{D}}}_{{\rm {m}}}={{PET}}/({P}_{{\rm {l}}}+M)$$

(4)

$${{\mathcal{E}}}_{{\rm {m}}}={{ET}}/({P}_{{\rm {l}}}+M)$$

(5)

This definition excludes frozen precipitation that does not melt throughout the month and includes melt that stems from frozen water storage that may have formed through snowfall in months prior.

We find that despite the discussed strong increases of ET in winter, ${{\mathcal{E}}}_{{\rm {m}}}$ and ${{\mathcal{D}}}_{{\rm {m}}}$ (Fig. 5e and f) reduce in winter months in the eastern US and the mountainous west at up to −20% K⁻¹ while increasing in spring. This counter-intuitive result is explained by seasonal changes to the liquid water supply P_l + M, which outweigh the strong changes in ET (see Supplementary Fig. S10 and decomposition in Supplementary Fig. S11). During winter months, liquid water supply for ET is enhanced with warming as precipitation shifts from frozen to liquid and snow melts throughout the season, shifting the winter-time mountainous west from a water-limited ET regime to an energy-limited one (triangles in Fig. 5f). During spring, reduced snow-cover reduces melt and hence liquid water supply, increasing ${{\mathcal{E}}}_{{\rm {m}}}$ and ${{\mathcal{D}}}_{{\rm {m}}}$.

The hydrological regime shift of the winter-time mountainous west towards an energy-limitation of ET occurs despite an enhanced energy supply in winter, as shown by the relative change in the net surface energy imbalance F_net (Fig. 5g), which we normalize by the latent heat of vaporization ${{\mathcal{H}}}_{{\rm {vap}}}$ and ET_CTRL to obtain comparability to ET changes. The increased F_net in winter can largely be attributed to the shortwave component, which is strongly controlled by changes in surface albedo through the loss of reflective snow (Supplementary Figs. S10 and S12). This finding is in agreement with previous studies over the western US that argue towards loss of reflective snow energetically fueling ET under warming^91,105. Our results highlight how this increased energy-supply for ET is present but dominated by an enhanced water-supply that alters the winter-time mountainous west to an energy-limited ET regime.

Relative changes in winter-time F_net in the other regions are weaker than over the mountainous west (Fig. 5g) as the energy balance of the surface is less dominated by snow. In fact, over the eastern US most of the increase in F_net is explained through the longwave component, which is mostly driven by the water vapor feedback as cloud changes are small and towards reduced cloud cover in all regions (Supplementary Figs. S10 and S12). Overall, these less pronounced changes to F_net under an already existing energy limitation on ET in the CTRL simulation yield overall weaker responses of ET to warming compared to the mountainous west.

Finally, having discussed the seasonal changes in P and ET with warming across CONUS, we turn to runoff R (Fig. 5h), the direct precursor of streamflows. R changes exhibit a strong seasonality over the mountainous west with increases of around 10% K⁻¹ in winter and summer, and a strong reduction near 20% K⁻¹ in spring. Considering that in absolute terms most R is produced in spring, we find a significant reduction of the annual mean R of −4.1% K⁻¹ (see abs. changes in Supplementary Fig. S10). The increase in winter- and summer-time R is nonetheless worth noting, given that in both seasons ET is found to increase at a higher rate than P (Fig. 5c and d). In winter months, the increased supply of liquid P and melt explains increases in both R and ET (Supplementary Fig. S10). The increase of R in summer despite a reduction in mean P (Fig. 5c) is most likely explained by a shift towards less frequent but more intense P events. Over the west coast, R changes also have a clear seasonal component, albeit at a lower magnitude than over the mountainous west, with increases at up to 5% K⁻¹ in winter. Over the Eastern US, R increases between 5% and 10% K⁻¹ throughout the year with a slight variation between a weaker increase in March due to loss of melt and a stronger increase in May due to increased liquid precipitation, particularly from ARs (Fig. 4). The stronger increase in R over the east compared to the west coast can be attributed to the overall stronger increase in P over the east under similar changes in ET, yielding a change in partitioning of P towards increased R/P and reduced ET/P as shown in Fig. 2b.

Relative importance of changes in antecedent upstream soil moisture and water inputs

With insights gained into the seasonal character of the processes driving changes in P, ET and R across CONUS, we now turn back to changes in high-flows and discuss how these characteristics tie in to changes in antecedent soil moisture, which is often regarded as a key predictor for R production^31,32,33,34. Specifically, we examine shifts in antecedent soil saturation ${{\mathcal{S}}}_{{\rm {a}}}$ of the top 1 cm of the soil, which describes the degree to which the pores of the soil’s top layer are filled with water prior to a precipitation or melt event. The upper-most layer is typically considered for this purpose because it controls production of R at the surface, which during an extreme precipitation or melt event is key for total R production³¹. Our approach is to take advantage of the day-by-day comparability between our CTRL and P2K simulations that is achieved through tightly nudged atmospheric winds, and allows us to separate identified high-flow days into those that occur only in the CTRL simulation, only in the P2K simulation or in both. This way, we can ask across these three categories of events how a change in upstream ${{\mathcal{S}}}_{\rm {{a}}}$ conditions may have contributed to a high-flow being only present in either CTRL or P2K, and put this change in relation to changes in the antecedent upstream soil-top water inputs ${{\mathcal{P}}}_{{\rm {a}}}$, i.e. the sum of antecedent upstream precipitation and melt (detailed the “Methods” subsection “Quantifying antecedent soil conditions and upstream drivers ”).

The bottom panels of Fig. 6 depict how many high-flow events, identified on a specific day and location, fall into the different categories of whether they occurred in either only the CTRL or the P2K simulation or in both, showing the total number and its breakdown into the various upstream drivers for each of the CONUS sub-regions. For each of the three categories, the upper panels of Fig. 6 display box-plots for distributions of antecedent upstream conditions (${{\mathcal{S}}}_{{\rm {a}}}$ and ${{\mathcal{P}}}_{{\rm {a}}}$) for all high-flow events in the CTRL and P2K simulations. It is evident that the dominant driver of high-flow events and its dependence on the climate state vary strongly across the sub-regions, as would be expected from our previous analysis of Fig. 3. Over the west coast, there are few high-flows that only occurred in the CTRL simulation, while most high-flows occur in both CTRL and P2K and are mostly driven by AR precipitation. Those high-flows that only occur in the P2K simulation show slight increases in ${{\mathcal{P}}}_{{\rm {a}}}$ and ${{\mathcal{S}}}_{{\rm {a}}}$ with warming, both of which act towards enhancing streamflows. As diagnosed in Fig. 4b, the additional high-flows over the west coast in the warmer climate occur mostly in winter during peak AR season, in which enhanced liquid precipitation and earlier snow-melt moisten soils, creating favorable conditions for enhanced runoff.

Fig. 6: Comparing magnitudes of antecedent soil moisture and upstream driver changes of high-flows.

Comparison of changes in antecedent soil moisture and upstream drivers for a) west coast, b) mountainous west and c) eastern US. For each sub-plot, the bottom panels show the regionally integrated distributions of high-flows identified in either CTRL or P2K simulation in categories of whether each high-flow, identified on a specific day and location, only occurred in the CTRL simulation, the P2K simulation or in both. The total number for each category is broken down into the attributed upstream drivers (AR precipitation, non-AR precipitation, melt). Upper panels show box-plots (black line at median, box-bounds at 25th and 75th percentiles, whiskers at 10th and 90th percentiles) of the total distribution (i.e. all upstream drivers) of upstream antecedent soil saturation ${{\mathcal{S}}}_{{\rm {a}}}$ (left y-axis) for high-flow events in the CTRL (orange) and the P2K (red) simulations, as well as sum of all upstream drivers ${{\mathcal{P}}}_{{\rm {a}}}$ (right y-axis) for high-flow events in the CTRL (light blue) and the P2K (dark blue) simulations in each category.

The strong reduction of high-flows over the mountainous west with warming (Fig. 3) is reflected in the bottom panel of Fig. 6b showing that most high-flows occur only in the CTRL simulation and are induced by melt. Looking at the difference in ${{\mathcal{S}}}_{{\rm {a}}}$ and ${{\mathcal{P}}}_{{\rm {a}}}$ for these cases between CTRL and P2K, we find that ${{\mathcal{P}}}_{{\rm {a}}}$ reduces significantly in the warmer climate while ${{\mathcal{S}}}_{{\rm {a}}}$ increases. Hence, the reason many high-flows over the mountainous west in the CTRL simulation do not exist in the P2K simulation is because of the loss of upstream water inputs ${{\mathcal{P}}}_{{\rm {a}}}$, in particular snow-melt, which outweighs the increase in increased ${{\mathcal{S}}}_{{\rm {a}}}$ that by itself favors high-flows in the P2K simulation. Those high-flows over the mountainous west that are only present in the P2K simulation are samples from a much more even distribution of precipitation and melt-induced cases (Fig. 6b, bottom panel), indicating a shift towards a more mixed and less snow-dominated hydrological regime. To a large extent, the newly arising high-flows in the P2K simulation are enabled by significantly enhanced ${{\mathcal{S}}}_{{\rm {a}}}$, which on the median increases from 0.2 in CTRL to 0.45 in P2K while the upstream drivers ${{\mathcal{P}}}_{{\rm {a}}}$ show a less significant increase. This strong increase in ${{\mathcal{S}}}_{{\rm {a}}}$ can be understood as a direct consequence of the discussed reduction in dryness index ${\mathcal{D}}$ (Fig. 5f) in winter months over the mountainous west with warming.

Over the eastern US, the largest number of high-flows occurs only in the P2K simulation, highlighting the strong sensitivity to warming in this region, which is driven to a similar degree by AR and non-AR precipitation. The high-flows that arise only in the P2K simulation are driven by a shift and a narrowing of the ${{\mathcal{S}}}_{{\rm {a}}}$ distribution towards higher ${{\mathcal{S}}}_{{\rm {a}}}$ values, as well as more extreme ${{\mathcal{P}}}_{{\rm {a}}}$, similar to the West Coast, but to a more pronounced degree. The enhanced sensitivity of ${{\mathcal{S}}}_{{\rm {a}}}$ over the eastern US compared to the west coast is likely caused by the fact that over the west coast, ${{\mathcal{S}}}_{{\rm {a}}}$ is already close to saturation in the CTRL simulation for most high-flows, while over the eastern US ${{\mathcal{S}}}_{{\rm {a}}}$ increases in winter months as the dryness index ${{\mathcal{D}}}_{{\rm {m}}}$ reduces significantly (Fig. 5f).

Discussion

We conducted a counter-factual warming experiment with the GFDL moderately high-resolution coupled atmosphere-land model AM4.0/LM4.0 to derive a physical understanding of the relation of the precipitation and streamflow responses to warming across CONUS, with particular focus on high-flows that are indicative of flooding. By nudging atmospheric winds in both our control and warming simulations, our approach isolates the thermodynamic component of the total response, focusing attention of this study on the implications of the first-order and most well-understood part of the total precipitation response on streamflows. We first quantified the precipitation and streamflow responses on the mean and the extremes across CONUS, elucidating their regionally varying relationship through the varying partitioning of ET and R. We then attributed the relation of precipitation and streamflow responses to changes in upstream water inputs, distinguishing AR and non-AR precipitation as well as melt, seasonal energy and water constraints on ET and associated implications for antecedent soil moisture conditions prior to high-flows.

We identify three sub-regions of CONUS that exhibit substantially varying streamflow responses to a comparatively homogeneous precipitation response. Over the West Coast, the streamflow response is positive but falls below precipitation scaling, approaching only up to 4% K⁻¹ in the extremes. Over the Eastern US, streamflow scales beyond precipitation, approaching 10% K⁻¹ and over the mountainous western US, streamflows dwindle, approaching −10% K⁻¹ despite significant increases in annual mean precipitation, particularly from ARs. We associate these regionally varying relationships of the thermodynamic precipitation and streamflow responses to varying hydrological regimes in terms of dominance of snow compared to liquid precipitation, as well as energy and water limitations of ET, which are embedded in regionally distinct seasonalities.

The most striking dichotomy between dwindling streamflows across the mountainous west and increasing streamflows elsewhere can be attributed to the dominance of springtime snow melt in driving the regional hydrological dynamics over the mountainous west. Reduced accumulation of snow throughout the winter months diminishes melt in spring, the season of most significant runoff production. As a consequence of reduced snow-cover in winter, the surface energy balance shifts towards higher PET through enhanced short-wave absorption. At the same time, liquid water supply increases with enhanced winter-time liquid precipitation and melt, yielding an overall moistening of the mountainous west in winter, fueling ET increases at about double the rate of the mean precipitation response and also in winter-time runoff. Through these changes, the winter-time mountainous west shifts from a water-limited ET regime to an energy-limited one with warming. We find that the moister soils not only enable enhanced ET, but also create favorable conditions for high-flows during winter at a more even distribution among driving AR precipitation, non-AR precipitation and melt. However, in the annual mean, these increases do not balance the significant reduction of melt-driven runoff in spring, resulting in a net annual runoff loss of around −4.1% K⁻¹.

While both the eastern US and the west coast exhibit increasing streamflows with warming, the increase is significantly stronger across the East. Over both regions, liquid precipitation is identified as the main driver for high-flows, with ARs contributing about two-thirds over the west coast and about half over the east, while melt plays a secondary role. These proportions are insensitive to the use of a different AR tracking algorithm, enhancing confidence in the significant role ARs play in thermodynamically scaling as a strong contributor to high-flows with warming. However, we need to recognize that other types of precipitation systems, such as meso-scale convective systems or hurricanes, have not been assessed in this study, and possible misrepresentations of those could bias the partitioning towards the relatively well-captured ARs. Expanding the attribution framework of this study to more types of precipitation systems denotes an interesting future perspective.

To explain the diagnosed difference in the magnitude of the streamflow increase between the West Coast and the eastern US, our results suggest two major reasons. Firstly, the partitioning of water losses between ET and R vary significantly between the two regions, with R/P at 51 % over the west coast and about 28 % over the eastern US. This difference implies a stronger sensitivity of relative changes in R to changes in the partitioning of ET and P to warming over the east. Secondly, the precipitation increase over the east is simply at a higher magnitude than over the west (Fig. 5c), which in conjunction with almost identical increases in ET must yield a stronger runoff response over the east. This finding is in agreement with previous studies that identify the north-eastern US as the region with the highest precipitation increase over the last decades across the US^67,106,107.

This work highlights the complex system of regionally confined hydrological processes, which result in strongly varying streamflow sensitivities to warming. Changes in upstream water inputs shift the prediction problem of high-flows towards one of precipitation and away from melt, particularly over mountainous regions. ARs are identified as the strongest driver of high-flows across CONUS, not just the West Coast, and react sensitively to warming, implying a need for improving the predictability of ARs in particular. The presented work isolates the thermodynamic component of the total warming response, which, for precipitation extremes, is thought to dominate the more uncertain dynamic response, but may not capture significant contributions towards the regional streamflow response. Future research should focus on expanding the framework presented here towards incrementally including the dynamical response, the direct effect of CO₂ and its feedback with vegetation, aerosol forcing, as well as changes in SST patterns.

Land surface modelling advances to further reduce approximations of sub-grid heterogeneity and more sophisticated representations of river streamflow dynamics will help reduce uncertainties and more explicitly represent flooding. Another avenue of ongoing development is global storm resolving models (GSRMs) that run at grid-spacings of 4 km and less^108,109. While studies of land–atmosphere interactions based on such models are just starting, first results point to significant discrepancies with moderately high-resolution models with regard to the sensitivity of snow-cover to warming in mountainous regions¹¹⁰. Further exploring these differences, also in light of the currently simplified assumptions made in the land schemes of GSRMs, denotes an exciting future perspective.

Methods

Model setup and simulations

We use the coupled land–atmosphere model AM4.0/LM4.0 developed at NOAA’s Geophysical Fluid Dynamics Laboratory (GFDL), the main characteristics of which are described in the reference papers^46,58,59. The component models AM4.0 and LM4.0 are extensively used and validated in studying various aspects of the earth system, as they denote integral components of GFDL’s modeling suite, namely SPEAR (Seamless System for Prediction and EArth System Research)¹¹¹ and CM4 (Climate Model version 4)¹¹², as well as the physical baseline for more comprehensive representations of dust and chemical interactions within ESM4 (Earth System Model version 4)^113,114. A major simplification to those comprehensive modeling systems is that our AM4.0/LM4.0 simulations are forced by observed SSTs and sea ice concentrations, often referred to as AMIP (Atmospheric Model Intercomparison Project) mode¹¹⁵, which omits uncertainties revolving around ocean-atmosphere interactions that can result in biases of SST patterns.

We run AM4.0/LM4.0 in a moderately high resolution mode at around 50 km grid spacing, which on the model’s cubic-sphere grid is represented by 192 × 192 grid-boxes per cube face. This version of the model contributed to the CMIP6 HighResMip experiments³⁷ and our simulations follow the HighResMip protocol in being forced by daily varying observed SSTs, sea-ice concentrations and radiative gases. One major feature of our simulations is that we nudge atmospheric winds against the 6-hourly NCEP reanalysis⁶⁶ to achieve day-by-day comparability to observed weather and between our control and warming simulations, isolating the thermodynamic warming response. We conduct the nudging with a tight nudging timescale of 30 minutes, which assures that there is no significant change in circulation patterns between our control and warming simulations (Supplementary Fig. S4). The nudging is applied at a 30 min time scale by linearly interpolating the 6-hourly reanalysis data in time to the model timesteps and applying a tendency term to the wind-fields that is proportional to the interpolated NCEP winds and an exponential with an e-folding time of 30 min.

Our control (CTRL) and warming (P2K) simulations only differ in forcing by a homogeneous increase of daily SSTs by 2 K. A realistic future warming pattern can be decomposed into global mean and SST warming patterns. The goal of this study is to focus on the global mean SST warming component, which is robust in both models and observations, although the magnitude of global mean warming in response to a fixed radiative forcing remains uncertain¹¹⁶. Changes in SST warming patterns are challenging to capture in coupled climate models^117,118, implying uncertainties for precipitation changes with warming patterns^119,120 that we exclude from the scope of this study.

The land surface model LM4.0 discharges surface and sub-surface runoff across a grid-scale river network as fluxes of liquid water, ice and heat to connected grid-cells following the hydraulic geometry approach^60,61. This representation of rivers is idealized by assuming 1-way fluxes with the surrounding land and neglecting the effects of inundation. However, for the scope of this study to obtain a regional understanding of mean and high-flow responses to warming, this representation is adequate, given previous evaluation of the model for annual mean runoff^46,121, runoff ratios⁶¹, and monthly mean peak discharge in the Mississippi¹²².

Atmospheric river detection and evaluation

For AR detection, we follow the method of Guan and Waliser¹²³, which has previously been applied to AM4.0/LM4.0 simulations, with good agreement to observations^45,46. The algorithm is based on 6-hourly mean outputs of zonal and meridional vertically integrated vapor transport (IVT) to compute IVT magnitude at each grid-cell. The climatological seasonal 85th percentile of IVT (considering all 6-hourly timesteps within 5-month intervals centered around respective months) is calculated at each grid-cell and used as a threshold to identify possible AR objects, together with a lower absolute limit for IVT of 100 kg m s⁻¹. Following previous studies^46,124, we calculate separate IVT thresholds (i.e., 85th percentile of IVT) for the CTRL and the P2K simulation to eliminate changes in AR frequency purely due to Clausius-Clapeyron scaling of water vapor content in the atmosphere, which in itself does not imply enhanced AR activity or impacts. Changes in AR frequency with warming are shown in Supplementary Fig. S15, showing small changes of less than 1% K⁻¹ over the west coast and eastern US, but significant increases over the mountainous west. This regional dependence highlights that our tracking method is not subject to a strong sensitivity simply due to increases in water vapor following Clausius–Clapeyron.

After applying the IVT threshold, geometric conditions are applied to the AR candidate objects (i.e., spatial envelopes of regions of sufficient IVT). The geometric conditions include a minimum AR length > 2000 km, a length-to-width ratio > 2, as well as directional requirements with a minimum poleward component of IVT > 50 kg m s⁻¹ and a coherence of IVT direction with more than 50% of AR-candidate pixels required to have IVT directions within 45° of the mean AR-candidate object direction. The identified AR-objects are stored on a 6-hourly timestep. Since for the rest of our analysis we use daily data, we map the 6-hourly AR-masks to daily masks by considering a given day an AR-day if an AR is identified at least once on any of the 6-hourly timesteps. More detailed descriptions of how geometric requirements are implemented (i.e., through definition of an axis) can be found in the paper introducing the original algorithm¹²³. An additional criterion we apply for the AR condition is a minimum precipitation of 1 mm day⁻¹ (following ref. ⁴⁶).

We evaluated the resulting spatial distribution of AR frequency (Supplementary Fig. S14) and the AR contribution to mean and extreme precipitation across CONUS against observations (Supplementary Fig. S13). Both, the distributions of AR frequency and the climatological contribution of AR precipitation to annual mean and extreme precipitation is found to be very similar between our CTRL simulation and observations across CONUS.

Given uncertainties among AR tracking methods¹²⁵, we validated our results in the section “Attribution to upstream precipitation and snow melt” on ARs as upstream drivers of high-flows by reproducing them based on another AR tracking algorithm¹²⁶. A key difference of this algorithm is that it first calculates IVT anomalies by subtracting the climatological day-of-year mean IVT at each grid-cell and then uses an IVT-anomaly threshold rather than a threshold on absolute IVT (as opposed to ref. ¹²³). We calculate the IVT-anomaly threshold as the 94th percentile of 6-hourly anomalies from the day-of-year mean following previous studies^{126,127,128,129}. In addition, we require a minimum precipitation of 1 mm day⁻¹, as we do with the first AR-tracking algorithm. Further details about geometric requirements can be deduced from ref. ¹²⁶.

We find varying differences in AR frequency between the two algorithms depending on the region (Supplementary Fig. S14), finding a lower AR frequency over the mountainous west (as percentage of time: 5.8% based on¹²³ and 2.7% based on ref. ¹²⁶) and the west coast (11.3% based on ref. ¹²³ and 10.1% based on ref. ¹²⁶) and a slightly higher AR frequency over the eastern US (12.5% based on ref. ¹²³ and 12.6% based on ref. ¹²⁶). Despite these slight regional differences, the reproduced Fig. 3 and Fig. 4 based on the second AR tracking algorithm (Supplementary Figs. S8 and S9) look remarkably similar to the results based on the first algorithm, enhancing confidence in our conclusions.

Evaluation of the surface water balance

To evaluate the regional surface water balance of our AM4.0/LM4.0 CTRL simulation, we make use of an observationally deduced 1 km resolution water balance dataset available across CONUS from 1980 to present^95,96. The dataset is based on a Thornthwaite-style water balance model⁹⁴, which takes observed daily precipitation and temperature data from Daymet Daily data version 3⁹⁷ and computes daily runoff R, storage changes (soil water $\Delta {{\mathcal{S}}}_{{\rm {tot}}}$ and snow water equivalent ΔSWE) and ET. The water balance model is detailed by Terceck et al. ⁹⁵ and the data and code are freely available at NASA-Earthdata (https://cmr.earthdata.nasa.gov/search/concepts/C2674694066-LPCLOUD.html, last access: 07/27/2025).

To make the reference data comparable to our model output, we bi-linearly interpolate the dataset to the model grid and select the period 1980–2020. We first compute monthly averages of the fluxes the dataset provides, namely liquid precipitation P_l, ET, and R. Since frozen precipitation is not provided explicitly, we compute it as the residual of the monthly mean surface water balance:

$${P}_{{{f}}}={{ET}}+R+\Delta {{\mathcal{S}}}_{{\rm {tot}}}+\Delta SWE-{P}_{{\rm {l}}}$$

(6)

We then obtain total precipitation as P = P_l + P_f and deduce the regional, annual averages and spatial standard deviations across the west coast, mountainous west and eastern US in the same way as for the CTRL simulation and the results are presented in Fig. 2a. In addition, climatological maps comparing the ET/P and R/P across CONUS between the CTRL simulation and the reference dataset are provided in Supplementary Fig. S5.

Attribution of high-flows to upstream drivers

We identify daily high-flows from the output of the coupled grid-scale river network that is part of LM4.0 (Supplementary Fig. S1). We do so by defining a streamflow threshold based on the long-term 99.7th percentile of daily streamflows at each grid-point in the control simulation, which represents a recurrence interval of once per year. By applying this threshold to both CTRL and P2K simulations, we obtain a database of high-flow days at each location in both simulations. For each of these high-flow days, we conduct an attribution analysis to identify the major upstream source of water that led to the high-flow, distinguishing AR precipitation, non-AR precipitation and snow melt. For a given event, we first identify the upstream area, which for each grid-point is defined by the grid-scale river network. We then calculate the upstream area integral of the potential high-flow drivers, so we obtain their upstream time-series. We then conduct a lagged temporal correlation analysis between downstream streamflow at the grid-point where the high-flow occurred and the area-integrated upstream drivers.

To conduct the lagged temporal correlation analysis, we first calculate an event-specific drainage timescale τ_drain, which estimates the time it takes for water entering the upstream catchment to drain into the downstream grid-point:

$${\tau }_{{\rm {drain}}}=\frac{{v}_{{\rm {ds}}}}{\sqrt{A/\pi }}$$

(7)

where v_ds is the streamflow velocity at the downstream grid-point on the day of the high-flow and A is the upstream area of the catchment. Hence, τ_drain represents the time it would take for water in the center of a round catchment with area A to escape the catchment on a straight line at a fixed streamflow velocity v_ds. Although this assumption is very crude for estimating the actual drainage time of precipitation entering the catchment, we use it as a starting point for identifying a sufficient correlation of upstream drivers and downstream streamflows.

Knowing τ_drain for a given high-flow event, we now iteratively determine the best-correlated upstream driver. We do so by shifting the timeseries of upstream-integrated drivers by τ_shift ∈ (0, 1, …, 2 × τ_drain) days. For each iteration, we select a temporal window of downstream streamflow and upstream drivers of ±τ_drain around the day of high-flow. As a first check of whether a potential upstream driver could have caused the high-flow, we check whether the temporal integral over the selected temporal window of an upstream driver is larger than the temporal integral of streamflow. For example, in the selected window there must have been more precipitation upstream than discharge downstream, if precipitation is to be attributed the main driver of the discharge. We conduct this test for each τ_shift and each of the upstream drivers AR-precipitation, non-AR precipitation and melt as well as the sums of AR-precipitation and melt and non-AR precipitation and melt. If for any of these cases, the test is passed, we calculate the temporal correlation coefficient ρ_D,S of upstream driver and downstream streamflow in the selected temporal window. If ρ_D,S > 0.8, we attribute the high-flow event to the particular driver. Note the cases of combined AR- or non-AR precipitation with melt occurred so infrequently in our analysis that we omitted them in our discussions.

A schematic depiction of the attribution method’s workflow and some evaluation metrics are provided in Supplementary Fig. S6. The method is able to attribute about 35% of high-flows in both the CTRL and the P2K simulation, and works best for grid-points with small upstream basins, which is expected given the idealized assumptions about shape and drainage dynamics of the upstream basin as outlined above through the attribution method.

Quantifying antecedent soil conditions and upstream drivers

The characterization of antecedent soil saturation is embedded in our attribution method of upstream high-flow drivers (see Supplementary Fig. S16). For each high-flow event, we store the timeseries of the area sum of soil moisture at 1 cm depth over the upstream basin, which we call q_s, within the temporal window of ±τ_drain around the respective high-flow days. Using Eq. (8), we transform q_s into volumetric units, referred to as q_v, which is divided by soil porosity φ (Eq. (9)) yields soil saturation in 1 cm depth ${\mathcal{S}}$. Following Eq. (10), we calculate the antecedent upstream soil saturation as the minimum ${\mathcal{S}}$ within the period leading up to the high-flow event constrained by τ_drain.

$${q}_{{\rm {v}}}=\frac{{q}_{{\rm {s}}}}{1000\,{\rm{kg}}\,{{\rm{m}}}^{-2}}$$

(8)

$${\mathcal{S}}=\frac{{q}_{{\rm {v}}}}{\varphi }$$

(9)

$${{\mathcal{S}}}_{{\rm {a}}}=\min ({\mathcal{S}}(t))\quad {\rm{for}}\,{t}_{{\rm {HF}}}-{\tau }_{{\rm {drain}}}\le t < {t}_{{\rm {HF}}}$$

(10)

To compare ${{\mathcal{S}}}_{{\rm {a}}}$ between CTRL and P2K for events that only occur in CTRL and not in P2K or the reverse, we apply our high-flow attribution method based on the CTRL high-flow mask (i.e., identified days and locations of high-flows in CTRL) to the P2K simulation, as well as the P2K high-flow mask to the CTRL simulation. This way, we can obtain ${{\mathcal{S}}}_{{\rm {a}}}$ for the CTRL and P2K scenario for all events that denote a high-flow only in CTRL, only in P2K or in both.

The sum of upstream drivers ${{\mathcal{P}}}_{{\rm {a}}}$, made up of AR precipitation P_AR, non-AR precipitation P_nAR and melt M, depicted in Fig. 6, is derived analogously to S_a in that we consider the timeseries of the area-sum of upstream drivers leading up to the high-flow event. However, in this case, we consider the temporal integral of all drivers following Eq. (11).

$${{\mathcal{P}}}_{{\rm {a}}}=\mathop{\int}\nolimits_{t-{\tau }_{{\rm {HF}}}}^{{t}_{{\rm {HF}}}}({P}_{{\rm {AR}}}+{P}_{{\rm {nAR}}}+M)\,{\rm {d}}t$$

(11)

Calculation of potential evapotranspiration

Potential evapotranspiration (PET) can be considered an energetic upper bound of how much a surface can evaporate given its energy imbalance and in some definitions given specific atmospheric conditions. A wide variety of approaches to calculate PET exist, which are designed for specific vs. more broad applications and that have varying requirements towards the data^130,131. Here, we use the widely used Penman–Monteith Equation (Eq. (12)) over an open water surface¹³¹ to conduct our analysis of ET changes with warming in the section “Attribution to seasonal constraints on evapotranspiration”.

$${{PET}}=\frac{\Delta }{\Delta +\gamma }\frac{({F}_{{\rm {net}}}-G)}{{L}_{{\rm {v}}}}+\frac{\gamma }{\Delta +\gamma }\frac{6.43(1+0.536u)({e}_{{\rm {s}}}-{e}_{{\rm {a}}})}{{L}_{{\rm {v}}}}$$

(12)

where F_net is the radiative surface net energy imbalance, G is the sensible heatflux into the subsurface, both (in units of MW m⁻²); e_a and e_s are the 2 m actual vapor pressure and saturation vapor pressure (kPa); Δ is the derivative of e_s with respect to temperature T (kPa K⁻¹); u is the windspeed in 2 m height (m/s); L_v is the latent heat of vaporization (MJ kg⁻¹); γ is the psychometric constant (kPa K⁻¹). These metrics are calculated through the following equations:

$${L}_{{\rm {v}}}=2.501-0.002361T$$

(13)

$${e}_{{\rm {s}}}=0.6108\,\exp (17.27T/(T+237.3))$$

(14)

$$\Delta =4098{e}_{{\rm {s}}}/{(T+237.3)}^{2}$$

(15)

$$\gamma =0.0016286P/{L}_{{\rm {v}}}$$

(16)

$$u=0.75\ {u}_{10{\rm{m}}}$$

(17)

where T is 2 m temperature (°C) and P is atmospheric surface pressure (kPa) and u_10m is the windspeed at 10 m height, which is the reference height we obtain as output from the model.